Mandelbrot- und Julia-Mengen

Diese Seite gibt einen sehr kurzen Überblick über die Mandelbrot-Menge und die Julia-Mengen. Der Text ist sehr auf unsere Werkstatt ausgerichtet und stellt keinesfalls eine Abhandlung oder gar einen Lehrtext über Fraktale dar. Dazu gibt es viele andere Referenzen, von denen Sie einige auf der Seite Bibliographie finden.

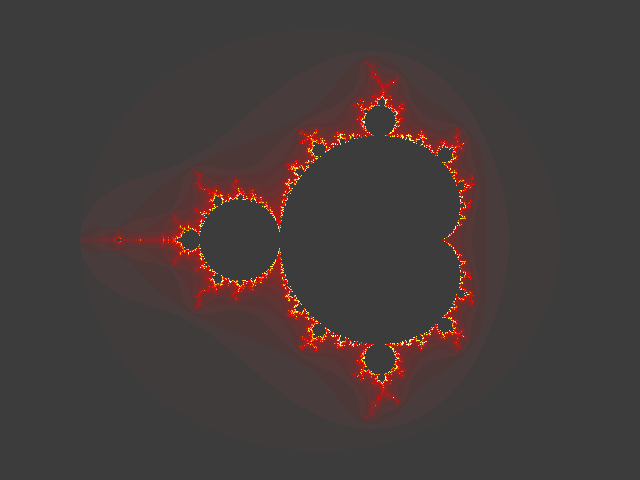
Wie werden Mandelbrot- und Julia-Mengen berechnet

So unglaublich es klingen mag, aber die folgende Mandelbrot-Menge (Apfelmännchen)

z und c sind dabei komplexe Zahlen, und die Bildebene ist die Ebene der komplexen Zahlen. Wie funktioniert diese Berechnung genau? Folgende Beschreibung ist eine Zusammenfassung aus [Dew89].

Die Formel wird erst lebendig, wenn man sie iteriert, d.h. wenn man mehrmals den alten Wert von z wieder in die Formel einsetzt um ein neues z zu berechnen. Die so entstandenen z-Werte, springen in der komplexen Ebene wild hin- und her, aber nach jeder Iteration hat sich das neue z etwas von seinem Vorgänger entfernt.

Eine schöne Parabel braucht Dewdney um die Iteration zu beschreiben. Er stellt sich die resultierende Zahlenfolge als Wanderbewegung des Ausgangspunktes vor. Dieser Ausgangspunkt sehnt sich nach der Unendlichkeit und es zieht ihn so immer weiter in die komplexe Ebene hinaus. Manchen komplexen Zahlen ergeht es wirklich so, andere wiederum bleiben auf ewig in einem Gebiet von sehr komplizierter Gestalt gefangen. Sie ahnen es: das Gebiet hat die Form des schwazen Bereiches im Inneren des Apfelmännchens.

Um ein Bild zu erhalten, macht man nun folgendes Experiment. Man setzt z gleich Null und variiert c systematisch über eine beschränkte Fläche. Für jeden Punkt in dieser Fläche untersucht man, ob der Punkt entkommen kann. Wenn der Punkt gefangen bleibt, färbt man ihn schwarz, entkommt er aber, so erhält er eine Farbe, die seine Fluchtgeschwindigkeit angibt. Es hat sich gezeigt, dass man mit folgender Bedingung Gefangene von Ausbrechern unterscheiden kann: überschreitet der Betrag von z einmal 2, so entkommt der Punkt. Um nicht ein endloses Programm zu erhalten, gibt man jedem Punkt eine bestimmte Anzahl Iterationen Zeit um zu entkommen. Genau betrachtet zeichnet man also immer nur eine Approximation der Mandelbrotmenge.

Was alles in der einfachen Formel z

z² + c steckt, zeigt sich erst, wenn wir c festhalten und z über eine beschränkte Fläche variieren. Zu jedem c das vorgegeben wird entsteht ein anderes Gebilde, eine sogenannte Julia-Menge. So hat also jeder Punkt im Apfelmännchen eine eigene Julia-Menge!

Pseudocode

Der Betrag von z berechnet sich als die Quadratwurzel von x² + y². Statt nun jedesmal die Quadratwurzel zu berechnen, quadrieren wir die Distanz. Zudem geben wir jedem Punkt 100 Iterationen um zu fliehen. Je grösser diese Zahl gewählt wird, desto genauer ist das entstehende Fraktal. 100 ist jedoch ein guter Kompromiss.

Der Grundalgorithmus

xx dient als Zwischenspeicher, damit der alte Wert von x in die Berechnung von y einfliessen kann. Jetzt müssen wir nur noch diesen Grundalgorithmus über einen Teil der komplexen Ebene schieben, und ihn in regelmässigen Abständen ausführen.

Wir zeichnen unser Bild auf einen Bildschirmausschnitt der cw Pixel breit und ch Pixel hoch ist. Zudem wird uns der Bereich der komplexen Zahlen über die wir c oder z variieren durch fx, fy, fw und fh vorgegeben. Dabei sind finden fx + ify die linke untere Ecke, fw und fh geben Breite bzw. Höhe des Bereiches an. Da wir in unserer Werkstatt stets Bilder berechnen, deren Höhe kleiner als deren Breite ist, bestimmt die Höhe die Schrittweite, mit der wir unseren Grundalgorithmus über die Ebene verschieben. Wir vermeiden eine Verzerrung des Bildes dadurch, dass wir die gleiche Schrittweite sowohl in x- als auch in y-Richtung haben. Natürlich könnte auch die Breite die Schrittweite bestimmen.

Rahmenprogramme für

Mandelbrot-Menge

Julia-Mengen

a  fx - Schritt
FOR j  1 TO cw
  a  a + Schritt
  b  fy - Schritt
  FOR i  1 TO ch
    b  b + Schritt
    x  0
    y  0
    [Grundalgorithmus]
  END
END

x  fx - Schritt
FOR j  1 TO cw
  x  x + Schritt
  y  fy
  FOR i  1 TO ch
    y  y + Schritt
    [Grundalgorithmus]
  END
END